
Zadanie Permutacje (prm)
Pomóż nam usprawnić bazę zadań!
Permutacje
Limit pamięci: 32 MB
Permutacja1
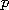 zbioru
zbioru 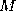 jest inwolucją wtedy i tylko wtedy, gdy
jest inwolucją wtedy i tylko wtedy, gdy 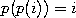 dla każdego
dla każdego 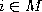 .
.
Wyrażeniem nawiasowym długości 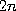 będziemy nazywać dowolne słowo długości
będziemy nazywać dowolne słowo długości 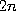 składające się wyłącznie ze znaków
'(' oraz ')'.
Wyrażenie nawiasowe jest poprawne, jeśli liczba nawiasów otwierających jest równa liczbie nawiasów zamykających, a w każdym prefiksie tego wyrażenia liczba znaków '(' jest nie mniejsza od liczby znaków ')'.
składające się wyłącznie ze znaków
'(' oraz ')'.
Wyrażenie nawiasowe jest poprawne, jeśli liczba nawiasów otwierających jest równa liczbie nawiasów zamykających, a w każdym prefiksie tego wyrażenia liczba znaków '(' jest nie mniejsza od liczby znaków ')'.
Powiemy, że permutacja 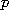 długości
długości 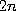 koduje wyrażenie nawiasowe o długości
koduje wyrażenie nawiasowe o długości 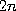 , jeśli
nawiasy otwierające w wyrażeniu (od lewej do prawej) są na pozycjach
, jeśli
nawiasy otwierające w wyrażeniu (od lewej do prawej) są na pozycjach 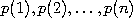 , zaś
zamykające - także od lewej do prawej - na pozycjach
, zaś
zamykające - także od lewej do prawej - na pozycjach 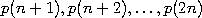 .
W szczególności, w takim przypadku zachodzi
.
W szczególności, w takim przypadku zachodzi 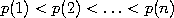 oraz
oraz
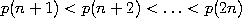 .
.
Znamy wartości pewnej permutacji 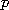 dla niektórych argumentów.
Należy stwierdzić, na ile sposobów można określić pozostałe wartości
dla niektórych argumentów.
Należy stwierdzić, na ile sposobów można określić pozostałe wartości 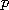 , tak by była ona inwolucją i kodowała poprawne wyrażenie nawiasowe.
, tak by była ona inwolucją i kodowała poprawne wyrażenie nawiasowe.
Wejście
W pierwszym wierszu standardowego wejścia znajdują się dwie liczby całkowite  oraz
oraz 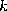 (
(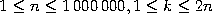 )
oddzielone pojedynczym odstępem.
W każdym z kolejnych
)
oddzielone pojedynczym odstępem.
W każdym z kolejnych 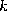 wierszy znajduje się jedna para liczb całkowitych oddzielonych pojedynczym odstępem;
wierszy znajduje się jedna para liczb całkowitych oddzielonych pojedynczym odstępem; 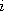 -ty
spośród tych wierszy zawiera liczby
-ty
spośród tych wierszy zawiera liczby 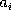 i
i 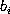 (
(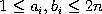 ), oddzielone pojedynczym odstępem
i oznaczające, że
), oddzielone pojedynczym odstępem
i oznaczające, że 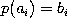 .
Wszystkie
.
Wszystkie 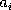 , jak również wszystkie
, jak również wszystkie 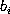 , są parami różne.
, są parami różne.
Wyjście
W pierwszym i jedynym wierszu standardowego wyjścia należy wypisać jedną liczbę całkowitą:
liczbę permutacji zbioru 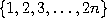 , które są inwolucjami, kodują poprawne
wyrażenie nawiasowe oraz spełniają podane na wejściu równości.
, które są inwolucjami, kodują poprawne
wyrażenie nawiasowe oraz spełniają podane na wejściu równości.
Przykład
Dla danych wejściowych:
3 4 1 1 2 2 4 3 6 6
poprawną odpowiedzią jest:
1
Wyjaśnienie do przykładu:
Jedyna permutacja, która spełnia wymogi zadania, to 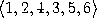 ,
a koduje ona następujące wyrażenie nawiasowe: (()()).
,
a koduje ona następujące wyrażenie nawiasowe: (()()).
1. Permutacją zbioru
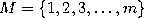 nazywamy dowolną funkcję różnowartościową
nazywamy dowolną funkcję różnowartościową 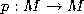 .
.
Autor zadania: Dariusz Leniowski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English